Deducción, inducción y abducción
Los caminos de nuestro cerebro son inescrutables y frecuentemente no somos conscientes de cómo construimos aquellos relatos a los que llamamos «realidad».
Para explicar esto, vamos a explicar cuáles son las tres principales formas de razonamientos lógicos que empleamos en nuestro día a día y dónde está la trampa constante que nos atrapa en forma de sesgos y prejuicios.
Estas tres vías son la deducción, la inducción y la abducción. Podemos simplificarlas mediante el siguiente esquema, donde cada una de las letras representa algo tan sencillo y a su vez ambiguo como una porción de la realidad. Para aterrizarlo mejor, vamos a imaginar que las letras son casos específicos (por ejemplo, personas, lugares, objetos…) o características que aplican a dichos casos (por ejemplo, cualidades de esas personas). 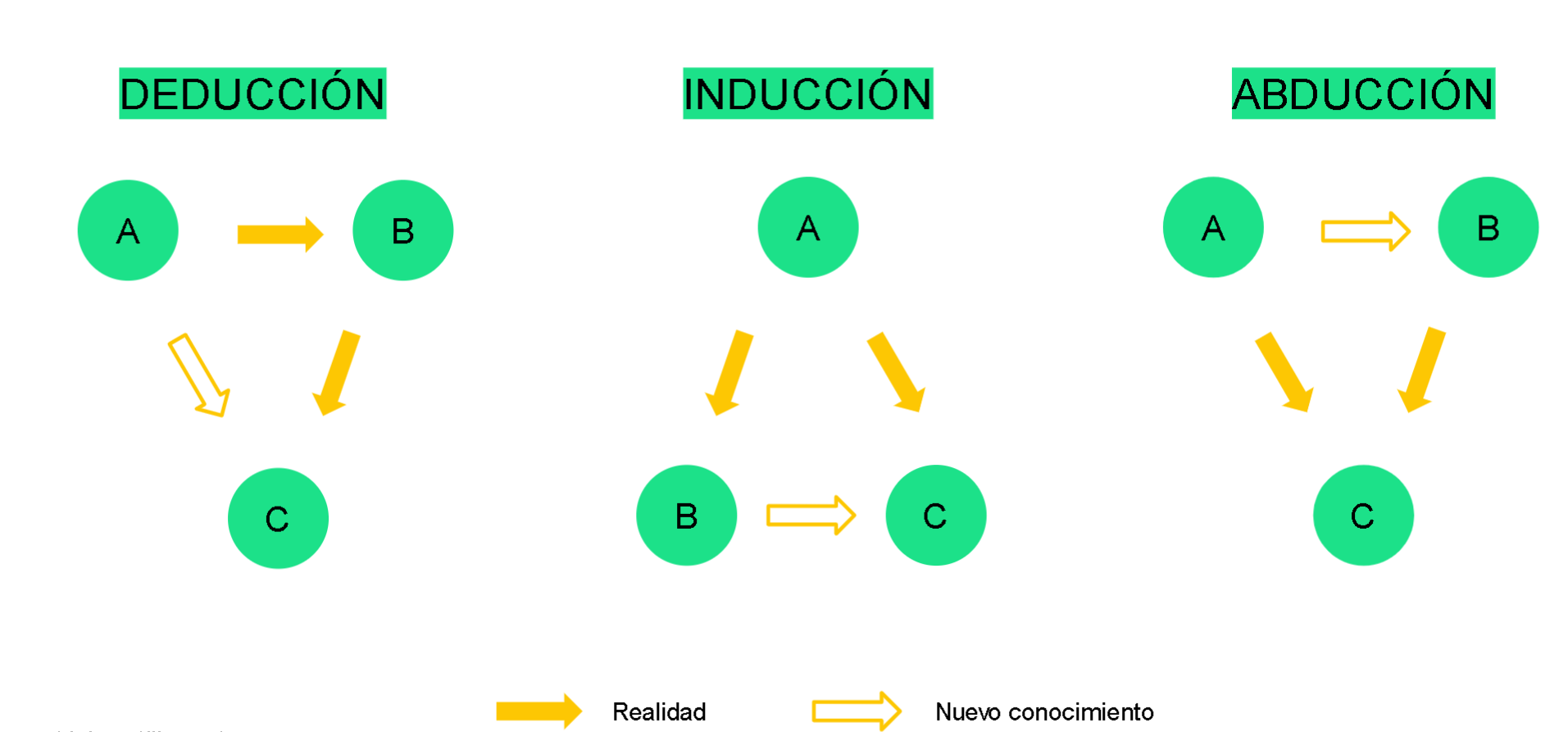
Por otro lado, las flechas representan la conexión que existe entre dichas letras. Las amarillas son aquellas conexiones evidentes y objetivas (fácilmente demostrables de una forma científica, semántica o empírica) mientras que las blancas son aquellos nuevos conocimientos que nosotros estamos construyendo en un proceso de aprendizaje. Es decir, tenemos tres piezas de información que ya presentan dos conexiones previas y nosotros buscamos cerrar el triángulo.
Deducción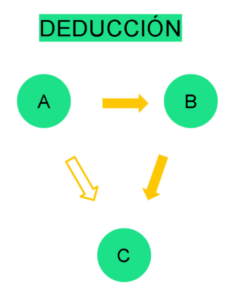
Lo primero que hay que destacar es que, de los tres métodos, la deducción es el único que NO nos permite generar nuevo conocimiento. Lo único que estamos haciendo es partir de dos relaciones lógicas concatenadas para generar una narrativa original que evita el paso intermedio, pero no aporta nada novedoso a lo que ya sabíamos.
Su expresión es «Si A lleva a B, y B lleva a C, por lo tanto A lleva a C»
Ejemplo: «A= Picasso; B= Málaga; C= España»
A→B: Picasso nació en Málaga. (Estamento cierto objetivamente demostrable)
B→C: Málaga está en España. (Estamento cierto objetivamente demostrable)
A→C: Picasso nació en España. (Nueva narrativa que no aporta realmente conocimiento)
Más ejemplos:
«Daniel es autónomo; los autónomos pagan una cuota; Daniel paga una cuota».
«El Athletic Club nunca ha descendido; los que descienden juegan en Segunda; el Athletic nunca ha jugado en Segunda»
Pensamos así en muchos ámbitos de nuestra vida. ¿Cuál es el principal problema? Más allá de que es un método discreto para adquirir conocimiento, si alguna de las asunciones que creemos objetivamente demostrable realmente no lo es, adiós deducción.
Ejemplos: ¿Málaga estaba en España cuando nació Picasso? ¿Hay autónomos exentos de cuota? ¿Puede un equipo descender dos categorías sin pasar por Segunda?
Inducción
Entramos en la chicha. La inducción y la abducción coinciden en que son razonamientos que nos llevan hacia NUEVO conocimiento. Como contraparte, asumimos el riesgo de estar equivocándonos, porque existe una parte de divergencia, de incertidumbre. Sin embargo, en este tipo de mecanismos se basa un conocimiento como el científico: no asentamos certezas, sino que evitamos refutaciones.
En el caso de la inducción, partimos de un caso específico (A) que tiene dos cualidades (B y C) y asumimos que existe una relación entre ambas. Se mueve desde lo particular a lo general.
Su expresión es «Si A es B y, además, es C, por lo tanto B siempre es C (y viceversa)».
Ejemplo: «A= Picasso; B= Pintaba cuadros; C= España»
A→B: Picasso pintaba cuadros. (Estamento cierto objetivamente demostrable)
A→C: Picasso nació en España. (Estamento cierto objetivamente demostrable)
B→C: Toda la gente que pinta cuadros ha nacido en España. (Nuevo conocimiento donde existe un margen más o menos amplio de incertidumbre)
También valdría C→B: Todos los españoles pintan cuadros.
¿Cómo podemos saber si nuestra nueva afirmación es realmente verdadera? Fácil: buscando el contraejemplo. Si encontramos un extranjero que pinta cuadros o un español que no lo hace, ya estamos refutando ambos razonamientos inductivos y todo el esquema se derrumba.
Este tipo de razonamiento queda muy bien explicado en el libro «Black Swan» de Nassim Taleb, llamado precisamente así porque todo el mundo creía que solo existían los cisnes blancos hasta que un día, de repente, se encontraron el primer cisne negro.
Más ejemplos:
«El PET es un plástico y, además, causa un alto impacto ambiental, por lo que todos los plásticos presentan tal impacto»
«Esta persona es inmigrante y ha cometido un delito, por lo que todos los inmigrantes cometen delitos»
Como se puede ver, el pensamiento inductivo también es un potencial criadero de bulos, manipulaciones y sesgos de confirmación, porque inconscientemente buscamos aquellas noticias que confirman esas asunciones recién construidas e inciertas en lugar de intentar hallar los contraejemplos que las desmonten.
Abducción
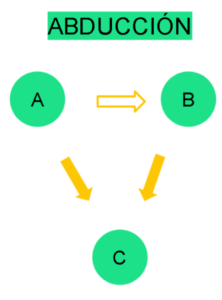
Finalmente, llegamos a la abducción, que es muy parecida a la inducción pero, al contrario, tenemos dos muestras independientes que comparten una misma cualidad, por lo que automáticamente pensamos que esos dos casos aislados realmente están conectados.
Al contrario que la inducción, va de lo general a lo específico.
Ejemplo: «A= Picasso; B= Estudiantes de bellas artes; C= Pintar cuadros»
A→C: Picasso pintaba cuadros. (Estamento cierto objetivamente demostrable)
B→C: Los estudiantes de bellas artes pintan cuadros. (Estamento cierto objetivamente demostrable)
A→B: Picasso estudió Bellas Artes. (Nuevo conocimiento donde existe un margen más o menos amplio de incertidumbre)
Si nos fijamos, la abducción puede parecer más sofisticada que la inducción porque, para comprobar si la nueva construcción de conocimiento es verdadera, no tenemos que buscar un fácil contraejemplo, sino realmente comprobar la nueva afirmación (lo he buscado y sí, Picasso estudió Bellas Artes, pero no habría sido llamativo si no lo hubiera hecho).
Más ejemplos:
«Los emprendedores montan empresas y Daniel monta una empresa, por lo que Daniel está emprendiendo»
«Esa persona mide más de 1’90 metros y es habitual que las personas de más de 1’90 metros jueguen al baloncesto, por lo que esa persona es probable que juegue al baloncesto».
Este último caso es curioso porque no estamos partiendo de una certeza absoluta como asunciones básicas sino que una de ellas es una probabilidad. Sin embargo, la estadística nos demuestra que, al menos en España, hay tal cantidad de personas más que juegan al fútbol respecto al baloncesto que, si seleccionamos a una persona al azar de 1’90 metros, sigue siendo más probable que juegue al fútbol que al baloncesto. Contraintuitivo, ¿verdad?
Realmente esto es otro sesgo que sucede porque recordamos con mayor facilidad aquellos casos que se salen de lo habitual («Efecto Von Restorff»). Por tanto, es más probable que tengamos en la cabeza a quienes juegan al baloncesto que a los que juegan al «mainstream» fútbol. Y si el deporte fuera mucho más minoritario, todavía es más probable que esa «rareza» quede destacada en conversaciones y capte nuestra atención.
Esto sucede igual cuando nos gusta una canción nueva y de repente parece que la ponen en todas las radios o que hablamos de un producto determinado y nos asustamos porque nos aparece en todos los anuncios. Simplemente, antes nuestro cerebro pasaba por alto esa información.
En el caso de la abducción, la clave es el tamaño de la muestra de cara a las generalizaciones. ¿Cuántos estudiantes de BBAA realmente pintan cuadros? ¿Cuántos emprendedores realmente montan empresas? ¿Cuántas veces te ha salido ese anuncio en Instagram respecto al total de anuncios que te has comido? Si estas respuestas tienden a 100%, estaremos más cerca de resolver el razonamiento abductivo con acierto que si partimos de imprecisiones, donde debemos contar con que existe una fuga estadística.
Como estamos enfocándonos en averiguar las condiciones de un caso particular, aquí no sirve buscar contraejemplos. De hecho, es importante asimilar que existe la probabilidad de que este caso observado pueda casualmente ser un contraejemplo. Incluso quizá el único existente. Perfectamente podría ser la única persona de +1’90m en el planeta que no juega al baloncesto y el enunciado seguiría siendo correcto.
En conclusión, tenemos tres métodos para obtener nuevas narrativas de conocimiento (dos basadas en realmente nuevo conocimiento y una en reformulación del ya existente). Pero estos procesos están plagados de trampas, donde las dos principales formas de esquivarlas son validar cómo de estadísticamente ciertas son las asunciones de partida y, después, tener en mente la búsqueda del contraejemplo en el pensamiento inductivo y comprobar particularmente el caso estudiado en el abductivo.
Aunque en procesos de diseño no perdamos de vista que, sin tirarnos el triple, nunca lograremos encestar. ¿O sí?